ダイクストラ法

経路探索アルゴリズム

続いて、カーナビなどで経路探索に用いらられる、ダイクストラ法について説明します。ダイクストラ法（Dijkstra's Algorithm）は、5日目で紹介した動的計画法のアルゴリズムの一つです。

このアルゴリズムは、ある地点から、別の地点まで、さまざまな経路の中から、最短経路を求めるために用いられるものです。

ダイクストラ法の考え方

では、ダイクストラ法での経路探索とは、どのようにすればよいのでしょう。そのためには、まず経路の表し方を定義する必要があります。ダイクストラ法で経路を探索するということは、経路は、いくつかの線が集まる接続点（ノード)

の間を、いかにして最低限のコストで結べるかという問題を意味します。

ノードとノードの間は、経路で結ばれており、スタートのノードから、ゴールのノードまで、この距離の合計が最低限になるようなノード間の接続の方法が見つかれば、それこそが、最短経路ということになります。

ダイクストラ法の実装

ダイクストラ法のアルゴリズム

ダイクストラ法の基本的な考え方は、「手近で明らかなノードから順次スタート地点からの最短距離を確定していき，その確定した情報をもとにさらに遠くまで確定していく」というものです。それを、より細かく書くと、以下のような手順になります。

  1. スタート地点の距離を0、他のノードの値を未定義に設定する。
  2. まだ確定されていないノードのうち，最小の値を持つノードを見つけ，確定ノードとする。
  3. 確定ノードからの伸びている経路をそれぞれチェックし，「確定ノードまでの距離＋経路の長さ」を計算し，そのノードの現在値よりも小さければ更新する。
  4. すべてのノードの距離が確定していなければ、2.に戻る

実際の検索例

では実際に、このアルゴリズムむの処理を簡単な実例に適用してみましょう。

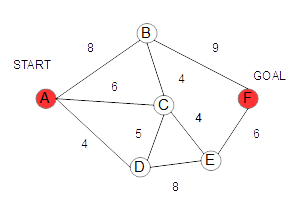初期状態 ノードA,B,C,D,E,Fを、左図のように設定したとします。ノードはそれぞれ、1つ、もしくは複数の経路で結ばれています。スタート地点のノードをA、ゴールをFとします。
各ノード間の距離は、ノードを結ぶ経路の上に記述されている数値とします。ゴールまでの距離は、ノードAからノードFに至るまでのこれらの数値の合計となります。
最終的に、その値が最小となるものが見つかれば、目的が達成されます。
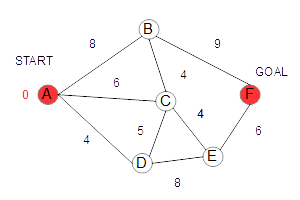スタート地点を0 スタート地点（A）の距離は、0となります。
当然ながら、このノードはすぐ確定となります。
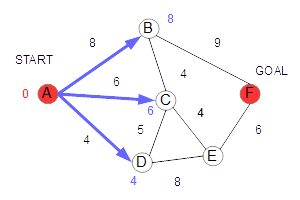Aからの最短距離を求める 次に、Aから最短の距離にあるノードを見つけます。
Aから直接行けるノードは、B,C,Dであり、そのうち最短のものはDとなります。
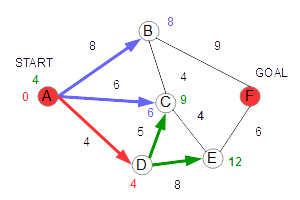Dから行ける道の探索 AからDまでの距離は、4なので、Dの距離はこの値で確定です。
続いて、Dから行ける、まだ確定していないノードの距離を求めます。
A→D→Cが、距離9、A→D→Eが距離12となります。
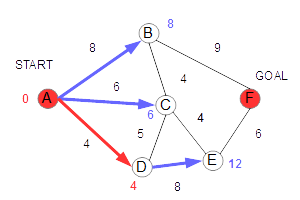C,Eの暫定値の確定 Cは、もともとAから直接Aから距離6で行けるので、この値は更新しません。
Eまでの距離は、ここではじめても止まったので、暫定値12を入れます。
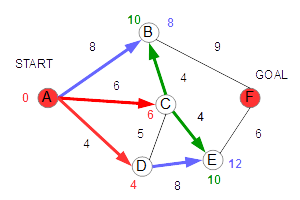Cが確定 この状態で、Cは確定します。
続いて、Cを経由してB,Eに至る距離を求めます。
A→C→Bが、距離10、A→C→Eの距離が10になります。
Bが確定Eが更新 Bは、Aから直接いける距離8のほうが近いので、値は更新されず、これで値が確定します。
また、Eの暫定値が12だったので、より短い10に更新されます。
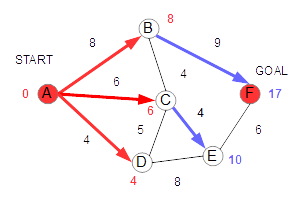
Cが確定 さらに、Cから行ける未確定のノードはEだけなので、ここで距離10が確定し、Eが確定します。
Bから行けるのはFだけなので、Fに暫定値17を代入します。
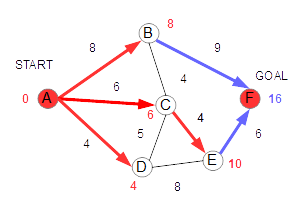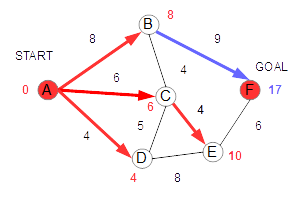
Fまでの道のり確定 続いて、Eを経由するFへの距離が16であることが分かります。暫定距離である17よりも短いので、この値が更新されます。
この距離は、もともと求めていた暫定距離の17よりも短いので、Fの値を更新します。
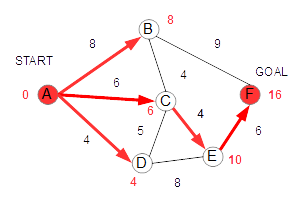初期状態 以上で、A,B,C,D,E,Fのすべての点の距離が確定します。これで検索作業は終了です。
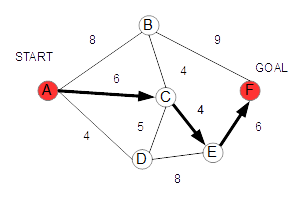終了 結果、A→C→E→F、距離16が、スタートからゴールまでの最短距離だということだとわかります。

ダイクストラ法の計算量

ダイクストラ法では、ノードの数をnとすると、ステップ数は O(n^2) となります。したがって、nの数が多いと、計算量が爆発するというデメリットがあるため、運用方法や、実装方法などを工夫する必要があります。

ただ、ヒープを使った場合は、経路の数をmとした時、O(nlogn+m) で求められます。実装方法を工夫すれば、より実用的な時間での検索が可能になります。